다양한 분류 알고리즘
4-1 로지스틱 회귀
주제: 로지스틱 회귀를 이용한 분류
목차
1. knn을 이용한 확률 분류
2. 로지스틱 회귀란?
3. 로지스틱 회귀를 이용한 이진 분류
4. 로지스틱 회귀를 이용한 다중 분류
knn을 이용한 확률 분류
knn을 사용하여 도미와 빙어 분류를 진행하겠습니다.
초반의 데이터 준비 및 모델 학습은 이전과 같은 과정이므로 설명은 생략하도록 하겠습니다.
# 데이터 준비
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv')
fish.head()
# 데이터 특성 확인
print(pd.unique(fish['Species'])) # 어떤 종류의 생선이 있는지 확인하기
# 인풋 데이터 만들기
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
# 타겟 데이터 만들기
fish_target = fish['Species'].to_numpy()
# 데이터 세트 나누기
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state=42)
# 표준화 전처리
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
# 모델 학습및 예측
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier(n_neighbors=3)
kn.fit(train_scaled, train_target)
print(kn.score(train_scaled, train_target))
print(kn.score(test_scaled, test_target))
knn모델에 학습이 완료되었으므로 테스트 케이스 데이터의 예측 결과를 보겠습니다.
print(kn.predict(test_scaled[:5]))
#---------------#
['Perch' 'Smelt' 'Pike' 'Perch' 'Perch']
다음과 같은 예측 결과가 나온 이유를 보기 위하여 확률을 알아보도록 하겠습니다.
# 확률 계산해보기
import numpy as np
proba = kn.predict_proba(test_scaled[:5])
print(np.round(proba, decimals = 4))
#---------------------#
[[0. 0. 1. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 1. 0. ]
[0. 0. 0. 1. 0. 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]]
predict_proba() 메서드에 관하여
해당 메서드는 분류 모델에서 클래스별 확률값을 반환합니다.
round를 이용하면 decimals 파라미터를 조정해 소수점을 조절할 수 있습니다.
위의 2차원 배열의 각 열은 classes 속성을 의미합니다.
따라서 1행의 데이터는 3번 클래스의 확률이 1인 것을 알 수 있습니다.
또한 3행의 3열 데이터의 값이 0.6667이 나온 이유는 knn모델이 계산한 근접 이웃 3개중 2개가 3열 클래스에 해당하고 1개가 5열 클래스에 해당하므로 나왔다는 것을 알 수 있습니다.
여기서 클래스가 대응되는 열은 다음 코드를 통해서 확인할 수 있습니다.
print(kn.classes_)
#-----------------#
['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
따라서 1열은 bream 클래스를 의미하는 것을 알 수 있습니다.
하지만 여기서는 주변 이웃의 수에 따라 확률이 제한적으로 나온다는 단점이 존재합니다.
이러한 문제를 해결하기 위해 로지스틱 회귀를 이용하도록 하겠습니다.
로지스틱 회귀란?
로지스틱 회귀는 이름은 회귀이지만 분류 모델입니다.
해당 알고리즘은 선형 회귀와 동일하게 선형 방정식을 학습하는 알고리즘입니다.
해당 선형 방정식은 z값과 각 계수(가중치) * 특성의 합으로 표현된다.
하지만 로지스틱 회귀는 각 클래스의 확률을 예측해야하므로 시그모이드 함수를 적용합니다.
σ(z) = 1 / (1 + e-z)
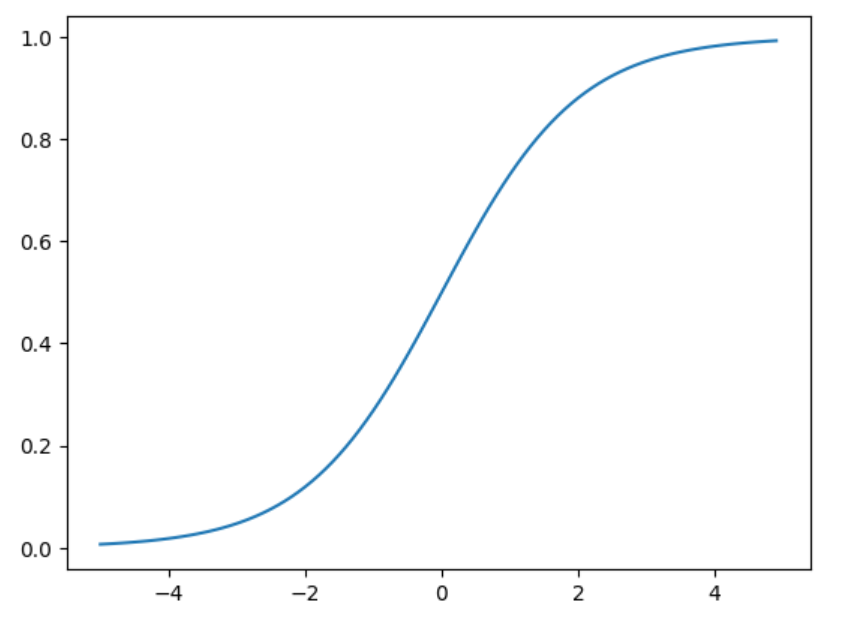
선형방정식을 통해 나온 z값을 시그모이드 함수에 대입하면 각 클래스의 확률을 0 ~ 1 사이로 예측가능합니다.
로지스틱 회귀를 이용한 이진 분류
이제 로지스틱 회귀 모델을 이용해 이진분류를 진행하도록 하겠습니다.
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
# 여러 종류의 생선이 있는 데이터에서 이진 분류를 위해 도미와 빙어의 데이터만 추출합니다
# bream_smelt_indexes 변수에 train_target과 크기가 같은 불리언 리스트를 할당합니다
# 이때 train_target == 'Bream' or train_target == 'Smelt' 로 인하여 도미와 빙어를 가지는 데이터의 인덱스에는 true가 할당됩니다
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]
# 불리언 인덱싱 적용하여 특정 데이터만 추출합니다
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)
# 로지스틱 회귀 모델에 데이터를 학습시킵니다
print(lr.predict(train_bream_smelt[:5]))
# 예측 진행
#----------------------#
['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
모델에 학습을 시킨 후 예측을 진행하니 다음과 같은 결과가 나왔습니다.
다음과 같은 결과가 나온 이유를 확률을 통해 알아봅시다.
print(lr.predict_proba(train_bream_smelt[:5]))
#--------------------------# #각 클래스에 대한 확률
[[0.99759855 0.00240145]
[0.02735183 0.97264817]
[0.99486072 0.00513928]
[0.98584202 0.01415798]
[0.99767269 0.00232731]]
print(lr.classes_)
#-------------------------# #각 열에 대응하는 클래스 파악
['Bream' 'Smelt']
위 결과를 통해 1행의 데이터는 1열(도미)의 확률이 높아 도미로 예측됨을 파악할 수 있습니다.
이제 로지스틱 회귀가 다음과 같은 확률을 내놓은 이유를 알아봅시다.
로지스틱 회귀도 선형 회귀와 같이 방정식이 있습니다.
그렇다면 방정식의 특성별 계수를 확인해 봅시다.
print(lr.coef_, lr.intercept_)
#---------------------------#
[[-0.4037798 -0.57620209 -0.66280298 -1.01290277 -0.73168947]] [-2.16155132]
위 방정식을 이용해 데이터들의 z값을 구해봅시다.
decisions = lr.decision_function(train_bream_smelt[:5])
print(decisions)
#----------------------------#
[-6.02927744 3.57123907 -5.26568906 -4.24321775 -6.0607117 ]
위에서 나온 z값들을 시그모이드 함수에 적용해보고 위의 각 클래스별 확률과 동일한지 확인해 봅시다.
from scipy.special import expit
print(expit(decisions))
#----------------------------#
[0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]
이를 통해 로지스틱 회귀를 이용한 이진분류를 학습하였습니다.
로지스틱 회귀를 이용한 다중 분류
이제 두개의 클래스가 아닌 총7개의 클래스로 분류를 진행해 보겠습니다.
# 로지스틱 회귀를 이용해 다중 클래스 분류하기
lr = LogisticRegression(C = 20, max_iter = 1000)
lr.fit(train_scaled, train_target)
print(lr.score(train_scaled, train_target))
print(lr.score(test_scaled, test_target))
#-----------------------------#
0.9327731092436975
0.925
C 파라미터란?
로지스틱 회귀 모델은 기본적으로 규제를 적용합니다.
여기서 C는 규제의 강도로 높을수록 규제를 완화합니다.
max_iter 파라미터란?
로지스틱 회귀 모델은 반복적인 알고리즘을 사용합니다.
해당 파라미터는 반복 횟수를 정의합니다.
위 결과를 통해 저희는 해당 모델의 과소적합/과대적합 문제가 없는것을 알 수 있습니다.
그럼 결과가 제대로 나왔는지 확인하는 과정을 진행하도록 하겠습니다.
print(lr.predict(test_scaled[:5]))
#--------------------------------#
['Perch' 'Smelt' 'Pike' 'Roach' 'Perch']
proba = lr.predict_proba(test_scaled[:5])
print(np.round(proba, decimals = 3))
#--------------------------------#
[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]
print(lr.classes_)
#--------------------------------#
['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
첫번째 데이터는 3열(perch)의 확률이 가장 높게 나왔으므로 perch로 예측된것을 볼 수 있습니다.
다음은 다중 분류일 경우 선형 방정식의 형태를 알아보도록 하겠습니다.
print(lr.coef_.shape, lr.intercept_.shape)
#---------------------------------#
(7, 5) (7,)
클래스의 종류가 7개이고 특성이 5개이므로 7행 5열의 배열로 계수가 출력되었습니다.
이 말은 이진분류에서 보았던 z 값을 7개를 계산한다는 의미입니다.
다중분류에서는 소프트맥스 함수를 이용해 z값을 확률로 변환시킵니다.
σ(z)i = ezi / ΣKj=1 ezj
다음은 z값을 소트프맥스 함수에 대입하여 나온 확률입니다.
# z값 구하기
decision = lr.decision_function(test_scaled[:5])
print(np.round(decision, decimals = 2))
#---------------------------------#
[[ -6.5 1.03 5.16 -2.73 3.34 0.33 -0.63]
[-10.86 1.93 4.77 -2.4 2.98 7.84 -4.26]
[ -4.34 -6.23 3.17 6.49 2.36 2.42 -3.87]
[ -0.68 0.45 2.65 -1.19 3.26 -5.75 1.26]
[ -6.4 -1.99 5.82 -0.11 3.5 -0.11 -0.71]]
# 소프트맥스 함수에 대입
from scipy.special import softmax
proba = softmax(decision, axis = 1)
print(np.round(proba, decimals = 3))
#-----------------------------------#
[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]
다음과 같은 과정으로 로지스틱 회귀를 이용해 다중 클래스 분류를 마쳤습니다.
4-2 확률적 경사 하강법
주제: 경사 하강법 알고리즘에 관하여
목차
1. 경사 하강법이란?
2. 손실 함수란? 2. 경사 하강법을 이용한 모델 학습
경사 하강법이란?
경사 하강법은 단어 그대로 경사를 따라서 내려가는 방법을 의미합니다.
자세한 의미는 함수의 값이 낮아지는 방향으로 각 독립변수들의 값을 변형시켜 함수가 최솟값을 갖도록 하는 독립변수를 탐색하는 방법입니다.
경사 하강법에도 방식에 따라 여러가지 종류가 존재합니다.
-
확률적 경사 하강법
확률적 경사 하강법은 전체 샘플을 사용하지 않고 딱 하나의 샘플을 훈련 세트에서 랜덤하게 골라 가장 가파른 길을 찾습니다. 자세하게 설명하자면 랜덤으로 샘플을 하나씩 선정하여 탐색을 하는 과정을 반복합니다.
해당 탐색은 전체 샘플이 모두 사용될 때까지 반복됩니다. -
미니배치 경사 하강법
해당 방법은 무작위로 몇개의 샘플을 선책하여 탐색을 진행합니다. -
배치 경사 하강법
해당 방법은 한번의 탐색을 위해 전체 샘플을 사용합니다.
손실 함수란?
경사 하강법에서 함수의 값이 낮아지는 방향으로 탐색을 진행하는데 여기서 함수가 손실 함수입니다.
손실 함수는 머신러닝 모델이 예측한 값과 실제 값의 차이를 나타내는 함수입니다.
손실함수에는 대표적으로 로지스틱 손실 함수가 있습니다.
다음은 로지스틱 손실 함수에 대한 설명입니다.
Log Loss = - (1/N) Σi=1N [ yi log(pi) + (1 - yi) log(1 - pi) ]
N은 전체 데이터의 수
y는 샘플의 실제 라벨(클래스)
p는 샘플에 대해 모델이 예측한 확률
경사 하강법을 이용한 모델 학습
# 경사 하강법을 사용한 분류 모델
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss = 'log_loss', max_iter = 10, random_state = 42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
#----------------------------------------#
0.773109243697479
0.775
사이킷런의 SGDClassifier 객체를 통해 학습을 진행합니다.
loss 파라미터란?
손실함수를 의미하며 log_loss는 로지스틱 손실 함수를 의미합니다.
경사 하강법의 또 다른 특징은 점진적 학습이 가능하다는 것입니다.
10번의 학습으로는 과소적합 되었으므로 학습을 이어서 진행하도록 하겠습니다.
sc.partial_fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
#------------------------------------------#
0.8151260504201681
0.85
partial_fit 메서드를 이용해 학습을 이어서 진행시켜 정확도를 향상시켰습니다.
여기서 최적의 반복횟수(에포크)를 찾아서 모델의 정확도를 더 향상시켜 보겠습니다.
에포크와 과대/과소적합
에포크의 횟수가 적다면 모델이 훈련 세트를 덜 학습하므로 과소적합 발생 가능
에포크의 횟수가 많다면 모델이 훈련 세트를 과도하게 학습하여 과대적합 발생 가능
따라서 에포크값에 변화를 주며 스코어 그래프를 그려 최적의 에포크를 찾는 과정을 이용합니다.
sc = SGDClassifier(loss = 'log_loss',random_state = 42)
train_score = []
test_score = []
classes = np.unique(train_target)
for _ in range(0, 300):
sc.partial_fit(train_scaled, train_target, classes = classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))
plt.plot(train_score)
plt.plot(test_score)
plt.show()
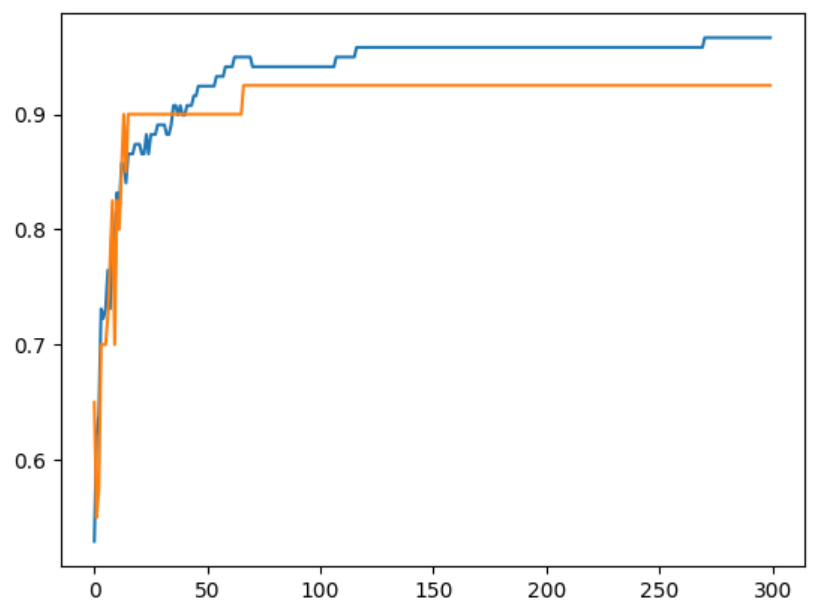
해당 그래프를 보면 에포크가 100일때 최적임을 알 수 있습니다.
sc = SGDClassifier(loss = 'log_loss',max_iter = 100, tol = None, random_state = 42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
print(sc.score(test_scaled, test_target))
#---------------------------------------#
0.957983193277311
0.925
에포크 값을 100으로 설정하고 학습을 진행하니 높은 정확도가 나옴을 볼 수 있습니다.
tol 파라미터란?
학습을 멈추지 않고 max_iter 값까지 자동으로 반복하도록 설정
이렇게 로지스틱 손실 함수를 통한 경사 하강법을 진행하였습니다.
로지스틱 손실 함수뿐만 아니라 힌지 손실등을 사용하여도 훈련을 진행할 수 있습니다.
이상으로 포스팅을 마치겠습니다.
