Affectionately

비지도 학습

6-1 군집 알고리즘

주제: 비지도 학습과 군집 알고리즘에 대한 이해

목차
1. 비지도 학습이란?
2. 비지도 학습을 이용한 데이터 분류

비지도 학습이란?

비지도 학습이란 별도의 타겟 데이터 없이 특징만을 가지고 데이터를 학습하는 것 입니다.

비지도 학습을 이용한 데이터 분류

데이터 준비

비지도 학습을 이용한 데이터 분류를 진행하기 위해 과일 데이터를 준비하였습니다.

import numpy as np
import matplotlib.pyplot as plt
!wget https://bit.ly/fruits_300 -O fruits_300.npy

fruits = np.load('fruits_300.npy') 

print(fruits.shape)

plt.imshow(fruits[0], cmap = 'gray')
plt.show()

# 출력 결과
(300, 100, 100)

fruits 데이터에는 사과, 파인애플, 바나나 이미지의 데이터가 2차원 배열의 형태로 존재합니다.

imshow 메서드를 이용하여 해당 2차원 배열을 이미지로도 확인해 봅시다.

해당 이미지는 fruits 데이터 중 첫번째 데이터를 이미지로 표현한 것입니다.

보통 흑백 샘플 이미지는 바탕이 밝고 물체는 짙은 색을 나타내지만 해당 이미지는 그와는 반대되는 것을 볼 수 있습니다.
이렇게 보이는 이유는 넘파이 배열로 이미지를 변환 할때 흑백 반전을 시켰기 때문입니다.

해당 이미지를 반전 시킨 이유는 컴퓨터가 바탕에 집중하지 않고 물체의 데이터에 집중하게 하기 위해 물체의 픽셀 값을 크게 해주고 바탕의 픽셀값을 낮춘 것입니다.

사과 말고 파인애플과 바나나의 이미지도 동일한 방식으로 확인해 봅시다.

fig, axs = plt.subplots(1, 2)
axs[0].imshow(fruits[100], cmap = 'gray_r')
axs[1].imshow(fruits[200], cmap = 'gray_r')
plt.show()

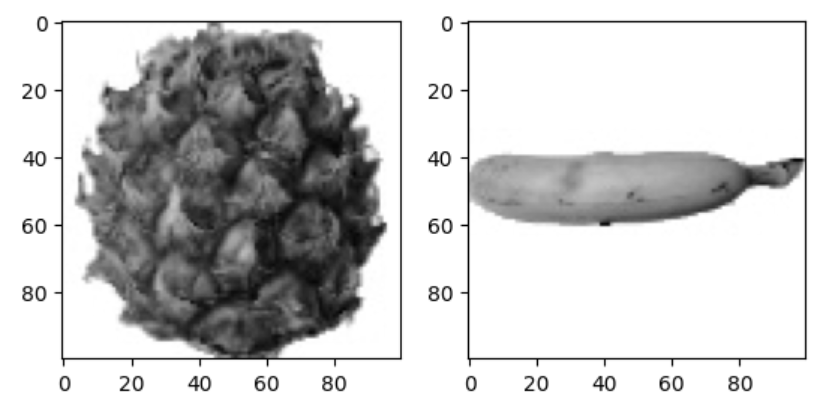
맷플롯립의 subplot 메서드를 사용하여 여러 개의 그래프를 배열 처럼 쌓을 수 있습니다.

이제 픽셀값을 이용해서 과일을 분류해보도록 합시다.

2차원 데이터를 다루기는 어려움이 있어 2차원 픽셀을 1차원으로 바꿉시다.

apple = fruits[0:100].reshape(-1, 100*100)
pineapple = fruits[100:200].reshape(-1, 100*100)
banana = fruits[200:300].reshape(-1, 100*100)

이제 해당 데이터를 가지고 클래스별 샘플의 픽셀 평균값을 계산해 봅시다.
axis = 1으로 설정하면 열을 따라 계산을 진행합니다.
따라서 각 샘플의 픽셀 평균값이 나오게 됩니다.

다음은 샘플의 픽셀 평균을 히스토그램으로 표현해 클래스별 특징을 살펴봅시다.

plt.hist(np.mean(apple, axis=1), alpha=0.8 )
plt.hist(np.mean(pineapple, axis=1), alpha=0.8 )
plt.hist(np.mean(banana, axis=1), alpha=0.8 )

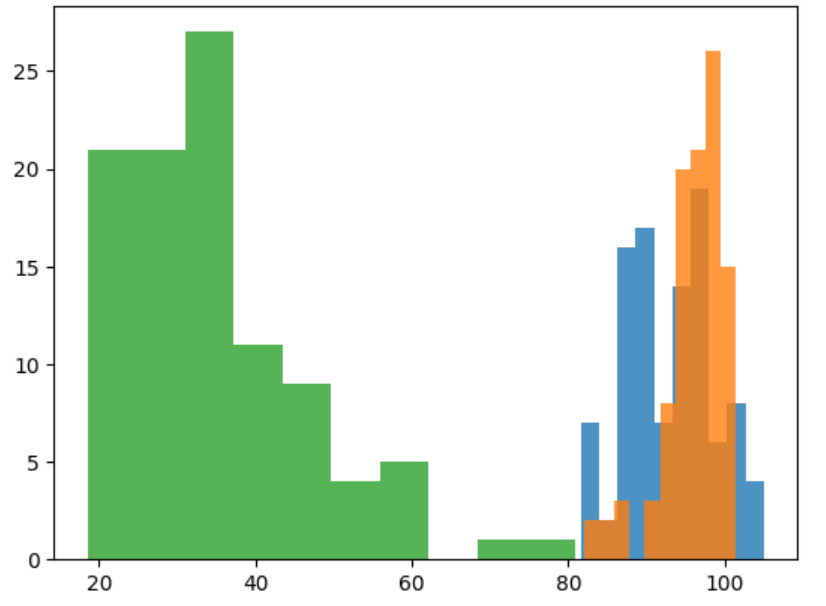
해당 히스토그램을 통하여 바나나는 평균값이 40아래에 집중된 것을 볼 수 있습니다.
하지만 사과와 파인애플의 구분에는 아직까지 어려움이 있습니다.

따라서 샘플의 평균이 아닌 픽셀의 평균을 구해봅시다.

fig, axs = plt.subplots(1, 3, figsize=(20,5))
axs[0].bar(range(10000), np.mean(apple, axis = 0))
axs[1].bar(range(10000), np.mean(pineapple, axis = 0))
axs[2].bar(range(10000), np.mean(banana, axis = 0))

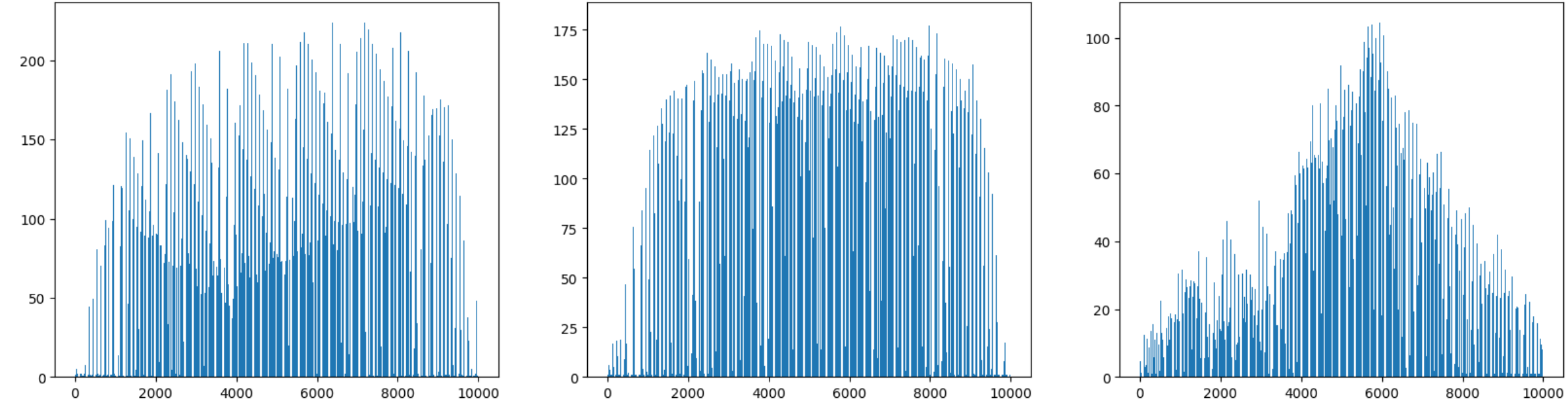
순서대로 사과, 파인애플, 바나나 그래프입니다.
사과는 사진의 아래쪽으로 갈수록 값이 높아지고 파인애플은 비교적 고르며 높다는 것을 알 수 있습니다.

픽셀의 평균값을 100*100 이미지로 출력하면 더 비교하기 좋습니다.

apple_mean = np.mean(apple, axis = 0).reshape(100, 100)
pineapple_mean = np.mean(pineapple, axis = 0).reshape(100, 100)
banana_mean = np.mean(banana, axis = 0).reshape(100, 100)

fig, axs = plt.subplots(1, 3, figsize = (20, 5))
axs[0].imshow(apple_mean, cmap = 'gray_r')
axs[1].imshow(pineapple_mean, cmap = 'gray_r')
axs[2].imshow(banana_mean, cmap = 'gray_r')

plt.show()

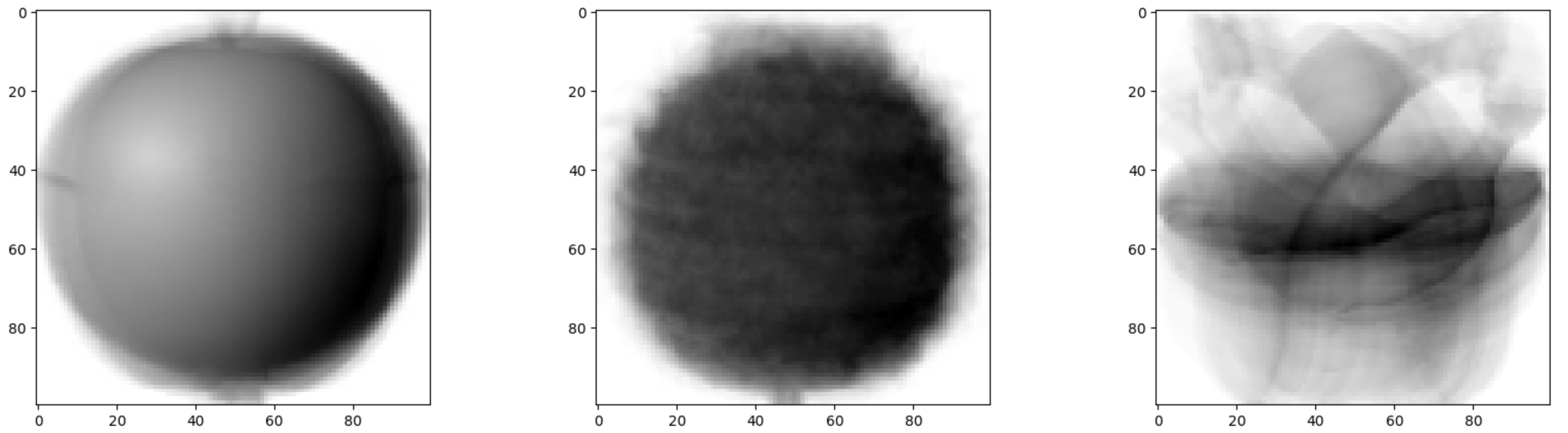
세 과일은 픽셀의 위치에 따라 값의 크기가 차이가 납니다.
따라서 이 대표 이미지와 가까운 사진을 골라낸다면 사과, 파인애플, 바나나를 구분 할 수 있습니다.

대표 이미지(픽셀의 평균)와 샘플의 절댓값 차이를 통해 클래스를 분류해 봅시다.

abs_diff = np.abs(fruits - apple_mean)
abs_mean = np.mean(abs_diff, axis = (1,2))

apple_index = np.argsort(abs_mean)[:100]
fig, axs = plt.subplots(10, 10, figsize = (10, 10))
for i in range(10):
  for j in range(10):
    axs[i, j].imshow(fruits[apple_index[i*10 + j]], cmap = 'gray_r')
    axs[i, j].axis('off')
plt.show()

사과와 절댓값 차이가 가장 적은 샘플들을 골라 출력하니 모두 사과가 나왔습니다.

이렇게 비슷한 샘플끼리 그룹으로 모으는 작업을 군집(클러스트링)이라고 합니다.
군집은 대표적인 비지도 학습 작업 중 하나입니다. 이렇게 군집 알고리즘에서 만든 그룹을 클러스터라고 합니다.

6-2 k평균

주제: k 평균 알고리즘을 이용한 비지도 학습 모델 설계

목차
1. k 평균 알고리즘이란?
2. k 평균을 이용한 분류

k 평균 알고리즘이란?

k 평균 알고리즘의 작동 방식은 다음과 같습니다.

1. 무작위로 k개의 클러스터 중심을 정합니다.
2. 각 샘플에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정합니다.
3. 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경합니다.
4. 클러스터 중심에 변화가 없을 때까지 2번으로 돌아가 해당 과정을 반복합니다.

k 평균을 이용한 분류

fruits_2d = fruits.reshape(-1, 100 * 100)

from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_2d)

print(np.unique(km.labels_, return_counts=True))

# 출력 결과
(array([0, 1, 2], dtype=int32), array([ 91,  98, 111]))

해당 코드는 과일 데이터를 k평균 알고리즘을 이용해 학습하고 각 샘플의 클래스를 확인하는 코드입니다.

여기서 n_clusters 매개변수는 클러스터의 개수입니다.

이제 각 클러스터가 어떤 이미지를 나타냈는지 그림으로 출력을 해봅시다.

def draw_fruits(arr, ratio = 0.4):
  n = len(arr)
  rows = int(np.ceil(n/10))
  cols = n if rows < 2 else 10
  fig, axs = plt.subplots(rows, cols, figsize = (cols*ratio, rows*ratio), squeeze = False)

  for i in range(rows):
    for j in range(cols):
      if i * 10 + j < n:
        axs[i,j].imshow(arr[i*10 + j], cmap = 'gray_r')
      axs[i,j].axis('off')
  plt.show()

draw_fruits(fruits[km.labels_ == 0])
draw_fruits(fruits[km.labels_ == 1])
draw_fruits(fruits[km.labels_ == 2])

레이블이 1인 클러스터는 바나나로만 이루어져 있습니다.
하지만 레이블이 2인 클러스터는 파인애플에 사과 9개와 바나나 2개가 섞여 있습니다.

k평균이 최종적으로 찾은 클러스터 중심은 cluster_centers_에 저장되어 있습니다.
해당 배열을 이미지로 바꾸어 출력해 봅시다.

draw_fruits(km.cluster_centers_.reshape(-1, 100, 100), ratio = 2)

이전 절에서 사과, 바나나, 파인애플의 픽셀 평균값을 출력한 것과 매우 유사합니다.

k 평균 클래스는 훈련 데이터 샘플에서 클러스터 중심까지 거리로 변환해 주는 transform 메서드를 가지고 있습니다.
이를 통해 샘플 하나를 확인해 봅시다.

print(km.transform(fruits_2d[100:101]))

print(km.predict(fruits_2d[100:101]))

# 출력 결과
[[5267.70439881 8837.37750892 3393.8136117 ]]
[2]

거리가 다음과 같이 나와 2번 클러스터로 예측되었습니다.

위 과정은 k를 3으로 설정하고 진행을 하였습니다.
하지만 비지도 학습의 경우에 따라 사전에 k값을 설정하기 어려운 경우가 존재합니다.
따라서 k값에 변화를 주면서 이니셔의 변화를 관찰해 최적의 k값을 찾을 수 있습니다.

이니셔란?
이니셔는 클러스터에 속한 샘플이 얼마나 가깝게 모여 있는지를 나타내는 값입니다.

inertia = []
for k in range(2,7):
  km = KMeans(n_clusters = k, random_state = 42)
  km.fit(fruits_2d)
  inertia.append(km.inertia_)

plt.plot(range(2,7), inertia)
plt.show()

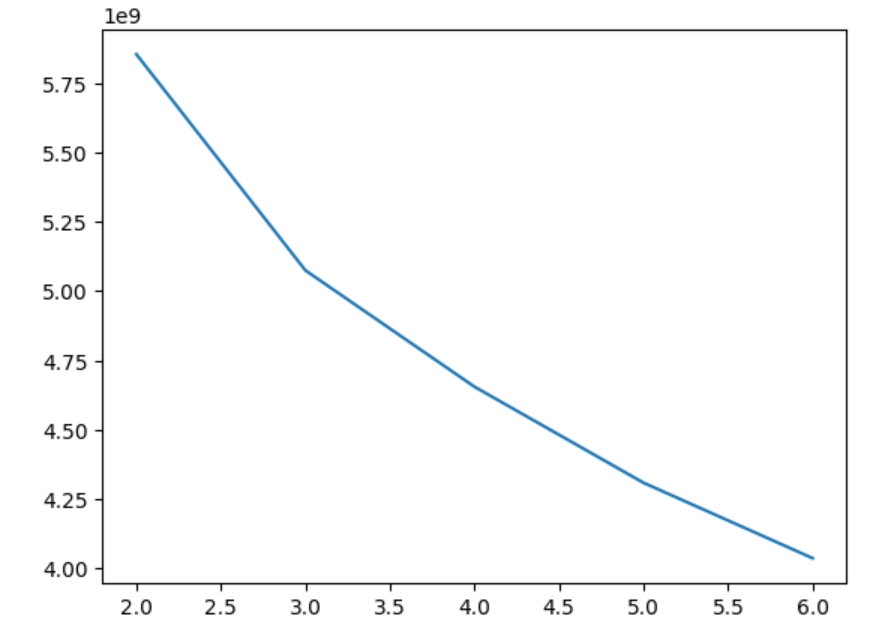
해당 그래프를 보면 k가 3인 지점에서 그래프의 추이가 변하는 것을 확인 할 수 있습니다.
따라서 k가 3인 지점이 최적의 클러스터의 개수입니다.

6-3 주성분 분석

주제: 차원 축소 알고리즘인 pca 모델 학습

목차
1. 차원과 차원 축소
2. pca

차원과 차원 축소

머신러닝에서 차원이란 특성의 개수와 같습니다.
머신러닝에서 차원을 줄일 수 있다면 저장공간을 크게 절약할 수 있습니다.

이를 위해 비지도 학습 중 하나인 차원 축소 알고리즘을 이용할 수 있습니다.

차원 축소는 데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이터 크기를 줄이고
지도 학습 모델의 성능을 향상시킬 수 있는 방법입니다.
또한 줄어든 차원에서 다시 원본 차원으로의 복원 또한 가능합니다.

PCA

주성분 분석은 데이터에 있는 분산이 큰 방향을 찾는 것입니다.

주성분 벡터는 원본 데이터에 있는 어떤 방향입니다.
따라서 주성분 벡터의 원소 개수는 원본 데이터셋에 있는 특성 개수와 같습니다.

from sklearn.decomposition import PCA
pca = PCA(n_components=50)
pca.fit(fruits_2d)

print(pca.components_.shape)

# 출력 결과
(50, 10000)

해당 코드는 pca 알고리즘을 이용해 50개의 주성분을 찾는 코드입니다.
n_components 매개변수를 이용해 찾고자하는 주성분의 개수를 조절할 수 있습니다.

주성분을 이미지로 표현해 봅시다.

draw_fruits(pca.components_.reshape(-1, 100, 100))

이 주성분은 원본 데이터에서 가장 분산이 큰 방향을 순서대로 나타낸 것입니다.
한편으로는 데이터셋에 있는 어떤 특징을 잡아낸 것으로 볼수도 있습니다.

주성분을 찾았으므로 이제 원본 데이터를 주성분에 투영하여 특성의 개수를 50개로 줄일 수 있습니다.

fruits_pca = pca.transform(fruits_2d)

앞에서 특성을 50개로 줄였습니다. 이제 이로 인해 어느정도의 손실이 발생했는지 알기 위하여
복원을 진행후 이미지로 표현을 해봅시다.

fruits_inverse = pca.inverse_transform(fruits_pca)

fruits_reconstruct = fruits_inverse.reshape(-1, 100, 100)
for start in [0, 100, 200]:
  draw_fruits(fruits_reconstruct[start:start+100])
  print("\n")

사과 클래스의 샘플을 살펴보니 대부분 적은 손실로 복원되었습니다.

주성분 분석에서 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값을 설명된 분산이라고 합니다.
pca클래스의 explined_variance_ratio_에 각 주성분의 설명된 분산 비율이 기록되어 있습니다.
당연히 첫번째 주성분의 설명된 분산이 가장 크게 나타납니다.
이 분산 비율을 모두 더하면 50개의 주성분으로 표현하고 있는 총 분산 비율이 나옵니다.

print(np.sum(pca.explained_variance_ratio_))

# 출력 결과
0.9215505997218063

앞에서 50개의 특성이 총 92 퍼센트가 넘는 분산을 유지하므로 원본 데이터의 복원이 잘 일어났습니다.

맷플롯립을 이용해 설명된 분산을 그래프로 출력합시다.

plt.plot(pca.explained_variance_ratio_)

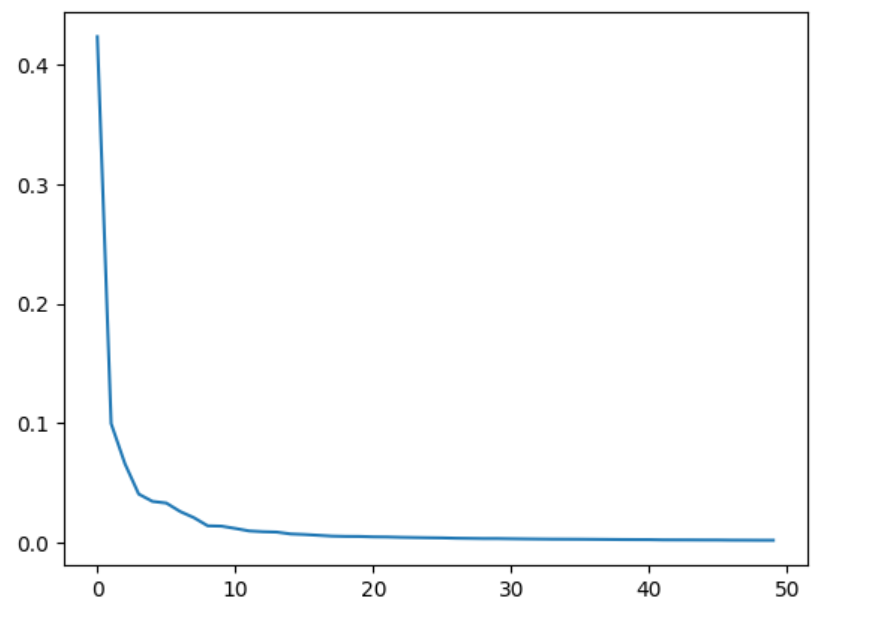
그래프를 보면 처음 10개의 주성분이 대부분의 분산을 표현하는 것을 알 수 있습니다.

이번에는 pca로 차원 축소된 데이터를 사용해 지도학습을 해보겠습니다.

from sklearn.linear_model import LogisticRegression

lr = LogisticRegression()

target= np.array([0]*100 + [1]*100 + [2]*100)

from sklearn.model_selection import cross_validate
scores = cross_validate(lr, fruits_2d, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))

scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))

# 출력 결과
0.9966666666666667
2.4502068519592286

1.0
0.06013579368591308

차원이 축소된 데이터로 훈련을 진행하면 정확도가 높아질 뿐만 아니라 훈력 속도 또한 증가하는 것을 볼 수 있습니다.

앞서 pca 클래스는 컴포넌트 매개변수에 주성분의 개수를 지정했습니다.
하지만 원하는 설명된 분산의 비율을 입력할 수도 있습니다.

pca = PCA(n_components=0.5)
pca.fit(fruits_2d)

print(pca.n_components_)

# 출력 결과
2

이를 통해 2개의 주성분만으로도 원본 데이터 분산의 50프로를 표현할 수 있습니다.
이를 통해 다시 학습을 진행합시다.

fruits_pca = pca.transform(fruits_2d)
scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))

# 출력 결과
0.9933333333333334
0.028298664093017577

2개의 특성만을 사용해도 99%의 정확도를 달성할 수 있습니다.

이번에는 차원 축소된 데이터를 사용해 k평균 알고리즘 클러스터를 찾아봅시다.

km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_pca)

for label in range(0,3):
  draw_fruits(fruits[km.labels_ == label])
  print("\n")

파인애플에는 어느정도 다른 과일과 혼동하는 경향이 있으나 나머지 클래스에 대한 분류는 잘 수행하였습니다.

또 다른 차원 축소의 장점은 시각화 입니다.
3개 이하로 차원을 줄이면 화면에 출력하기 용이합니다.
앞서 찾은 km.labels_를 이용해 클러스터별로 나누어 산점도를 그려봅시다.

for label in range(0,3):
  data = fruits_pca[km.labels_ == label]
  plt.scatter(data[:,0], data[:,1])

plt.legend(['pineapple', 'banana', 'apple'])
plt.show()

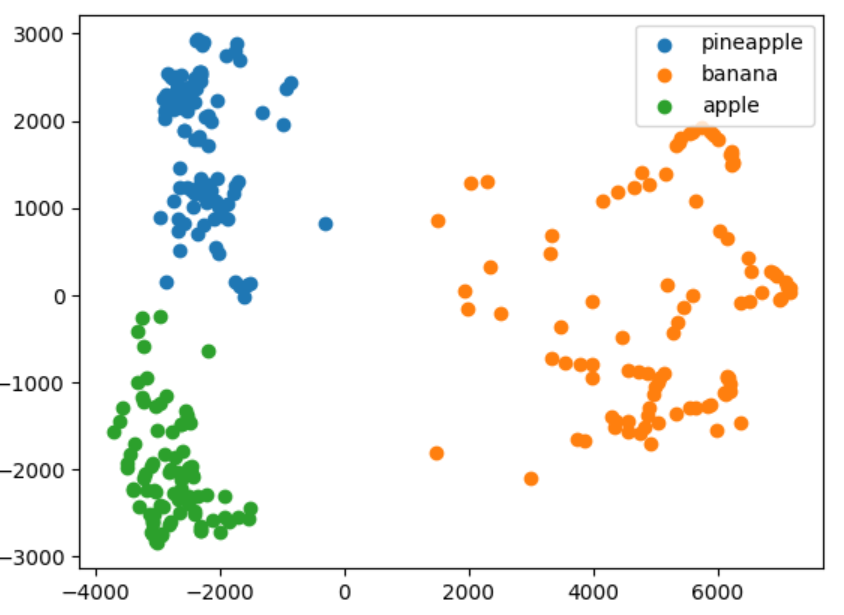
각 클러스터의 산점도가 잘 구분되는 것을 확인할 수 있습니다.

이상으로 포스팅을 마치겠습니다.