데이터 탐색과 시각화에 관하여
(1) 탐색적 데이터 분석 — 탐색적 데이터 분석이란 가공되지 않은 데이터를 있는 그대로 탐색하고 분석하는 기법입니다. 이 과정의 목적은 다음과 같습니다.
- 데이터의 형태와 척도 확인 (데이터의 형태는 구조, 타입, 차원, 형식등을 의미함/ 데이터의 척도는 속성을 의미함)
- 데이터의 평균, 분산, 분포, 패턴 등 특성 파악
- 데이터의 결측값 혹은 이상치 파악
- 변수간 관계 파악
다음은 라이브러리를 활용하여 EDA를 진행하였습니다.
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
sns.set(color_codes=True)
%matplotlib inline
df = pd.read_csv("C:/Users/kangmin/Desktop/hotel_bookings.csv")
df.head()
df.info()
df.describe()
df.skew()
sns.distplot(df['lead_time'])
head 메서드는 데이터 샘플을 확인하도록 도와주는 메서드로 5개의 행을 출력합니다
info 메서드는 각 칼럼의 속성과 결측치에 대한 정보룰 제공합니다
describe 메서드는 각 칼럼의 통계치(평균, 표준편차, max, min)에 대한 정보를 제공합니다
skew 메서드는 각 칼럼의 왜도(데이터 분포의 비대칭 정도)에 대한 정보를 제공합니다
sns.distplot(df[‘lead_time’]) 이 코드의 의미는 다음과 같습니다
데이터 파일의 lead_time 의 값을 가져와 특정 구간에 대한 데이터의 수를 히스토그램으로 시각화합니다
(2) 공분산과 상관성 분석
공분산은 각 변수의 변동이 얼마나 닮았는지를 표현한다
공분산을 구하는 방식은 다음과 같다
sigma 한 변수의 편차 * 다른 변수의 편차 / 데이터 샘플 수 - 1
공분산을 통하여 두 변수가 양의 상관관계를 나타내는지 아니면 음의 상관관계를 나타내는지 알 수 있다.
하지만 상관성이 얼마나 높은지에 관하여는 평가하기 어렵다.
피어슨 상관계수는 공분산과는 달리 상관성의 정도를 알 수 있다.
피어슨 상관계수를 구하는 방식은 다음과 같다
두 변수의 공분산 / 두 변수가 변하는 전체 정도
다음은 라이브러리를 활용하여 상관성을 분석하였습니다
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
df = pd.read_csv("C:/Users/kangmin/Desktop/winequalityN.csv")
df.head()
sns.set(font_scale = 1.1)
sns.set_style('ticks')
sns.pairplot(df, diag_kind = 'kde')
plt.show()
df.cov()
df.corr()
#히트맵 그래프 생성
# 숫자형 데이터만 선택
numeric_df = df.select_dtypes(include=[np.number])
# 상관 행렬 계산
corr = numeric_df.corr()
# 마스크 생성
mask = np.triu(np.ones_like(corr, dtype=bool))
# 플롯 설정
fig, ax = plt.subplots(figsize=(15, 10))
# 히트맵 생성
sns.heatmap(corr, mask=mask, vmin=-1, vmax=1, annot=True, cbar=True)
# 그래프 표시
plt.show()
sns.pairplot(df, diag_kind = ‘kde’)는 데이터 파일의 각 변수쌍에 대한 관계를 시각화하는 pairplot을 생성합니다.
pairplot은 변수쌍의 산점도를 나타냅니다.
diag_kind = ‘kde’는 대각선의 데이터를 kde 플롯을 사용하여 각 변수의 분포를 표현합니다.
cov 메서드는 공분산에 대한 정보를 제공한다
corr은 피어슨 상관계수에 대한 정보를 제공한다
위 히트맵 그래프의 코드는 하삼각행렬의 모양으로 변수간의 피어슨 계수를 시각화하여 보여줍니다.
(3) 시간 시각화
시간 시각화란 시간 흐름에 따른 데이터의 변화를 표현하는 것이다.
시간 시각화는 두가지 방식으로 표현 가능하다.
- 연속형 시간 시각화 - 선그래프가 대표적인 예로 시간 간격의 밀도가 높을때 사용된다. 데이터의 변화 추이를 파악하는데 용이하다. 하지만 데이터의 양이 많거나 변동이 심하다면 좋지 않다. 이럴 경우 추세선을 도입하여 패턴을 어느정도 안정화 시킬 수 있다.
- 분절형 시간 시각화 - 막대그래프, 점 그래프 등으로 표현한다. 시간의 밀도가 낮은 경우에 활용하기 좋은 방법이다. 값들의 상대적 차이를 나타내는 것에 유리하다.
다음은 시간 시각화 분석에 대한 코드이다.
import pandas as pd
# 데이터 로드
df = pd.read_csv("C:/Users/kangmin/Desktop/SuperStoreOrders.csv")
# 날짜 형식 자동 추론
df['Date2'] = pd.to_datetime(df['order_date'], errors='coerce')
# NaT 값 제거
df = df.dropna(subset=['Date2'])
# sales 열의 데이터 타입 확인 및 변환
df['sales'] = pd.to_numeric(df['sales'], errors='coerce')
df = df.dropna(subset=['sales'])
# 날짜 기준으로 정렬
df = df.sort_values(by='Date2')
# 연도 추출
df['Year'] = df['Date2'].dt.year
# 2018년 데이터 필터링
df_line = df[df.Year == 2018]
# 날짜별 매출 합계 계산
df_line = df_line.groupby('Date2')['sales'].sum().reset_index()
# 결과 확인
print(df_line.head())
(4) 비교시각화
비교 시각화란 그룹별로 특정 요소에 대한 차이를 나타내고자 할때 사용될 수 있다.
비교 시각화의 표현 방식은 다음과 같다.
- 히트맵 차트의 표현 방식
히트맵 방식은 그룹과 비교요소가 많을 때 효과적인 시각화 방식이다.

- 방사형 차트의 표현 방식
하나의 그룹에 관해 여러 특성을 표현할 때 효과적인 시각화 방식이다.

- 평행 좌표 그래프의 표현 방식
여러 그룹간의 비교우위를 표현할 때 효과적인 시각화 방식이다.

(5) 분포 시각화
분포시각화는 데이터를 파악하는 과정에 있어 용이하다.
데이터가 초기에 주어졌을 때, 변수들이 어느정도 비율로 구성되어 있는지 확인시켜주는 시각화 방식이다.
분포시각화는 양적 척도/질적 척도에 따라 구분된다.
-양적 척도인 경우 히스토그램을 이용하여 분포를 나타낼 수 있다.
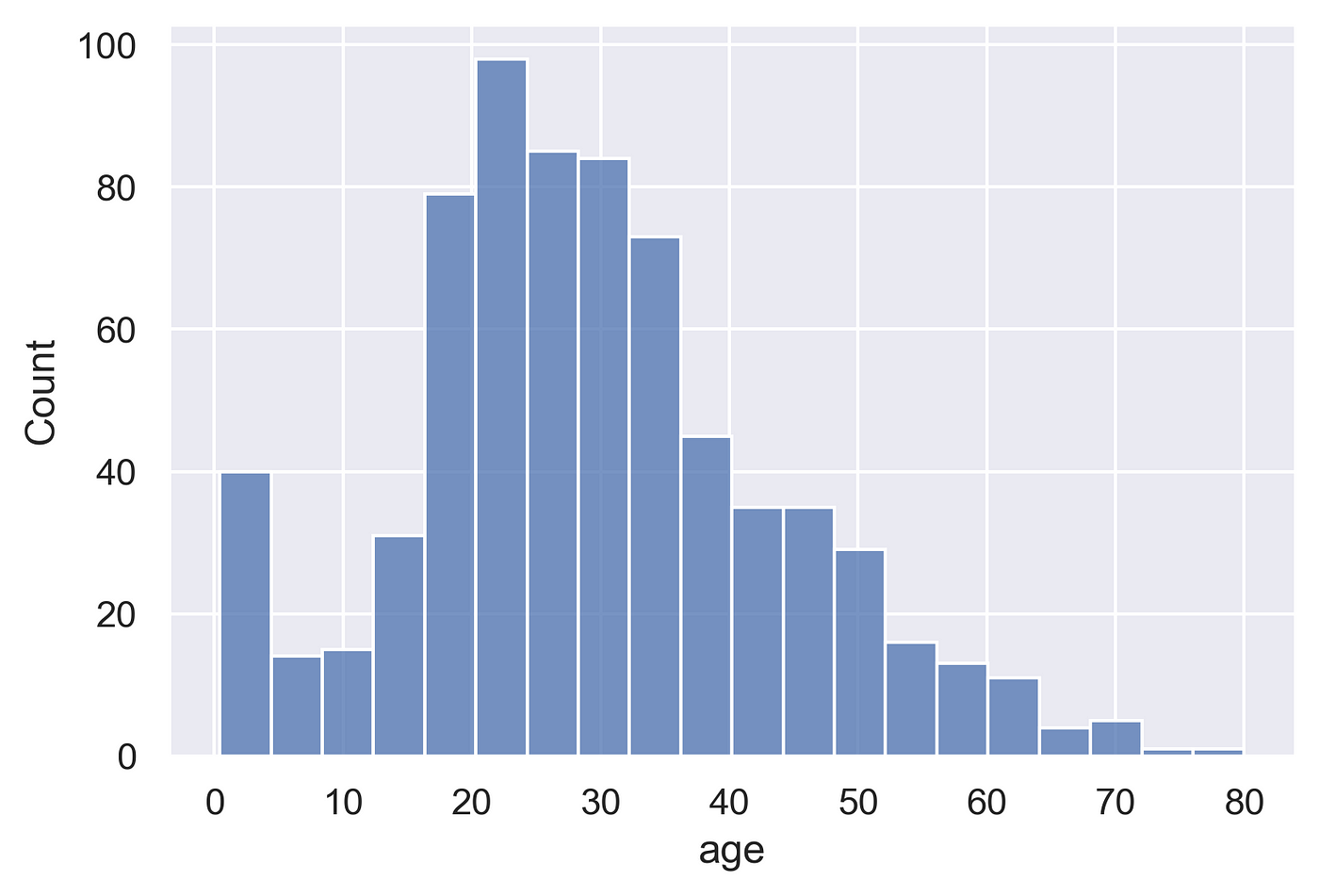 -질적 척도인 경우 파이차트나 도넛 차트를 활용하여 분포를 나타낼 수 있다.
-질적 척도인 경우 파이차트나 도넛 차트를 활용하여 분포를 나타낼 수 있다.
 -구성요소가 복잡한 질적척도 표현시에는 트리맵 차트를 이용하면 효과적이다.
-구성요소가 복잡한 질적척도 표현시에는 트리맵 차트를 이용하면 효과적이다.
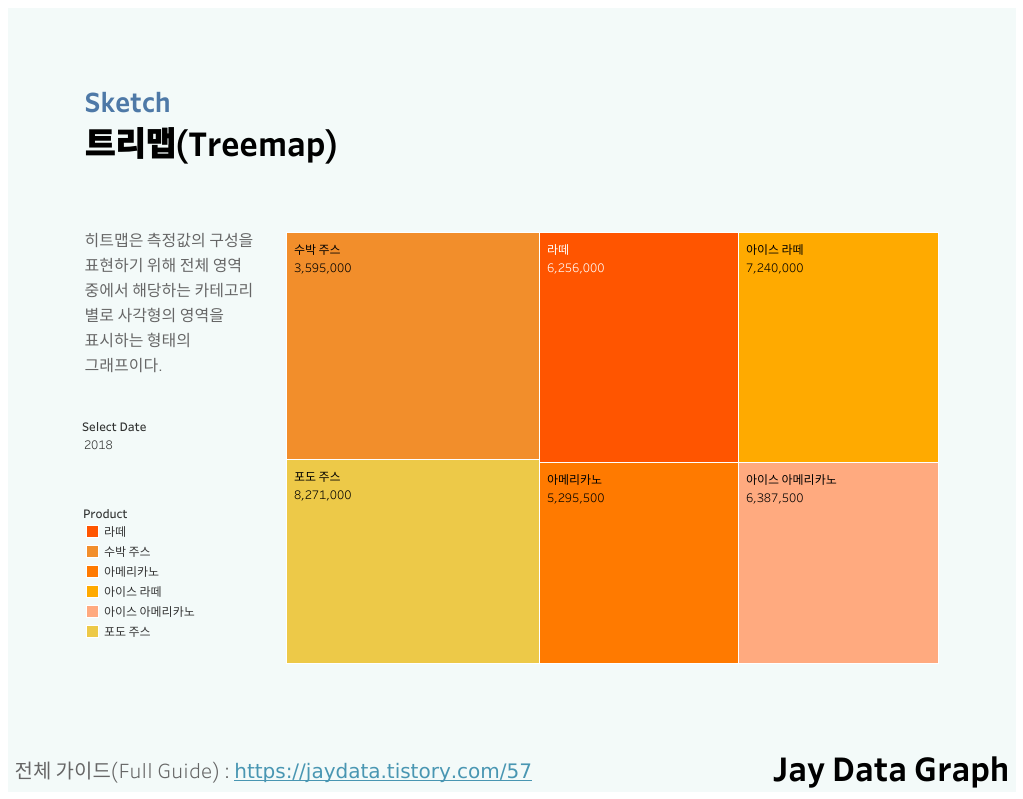
(6) 관계 시각화
관계시각화란 두 변수간의 관계를 시각화 하는 것이다.
대표적인 예로는 산점도가 있다.
다만 산점도는 두 개의 변수 간 관계만 표현 가능하다는 단점이 존재한다.
따라서 버블 차트를 이용해 세가지 요소의 상관 관계를 표현할 수 있다.
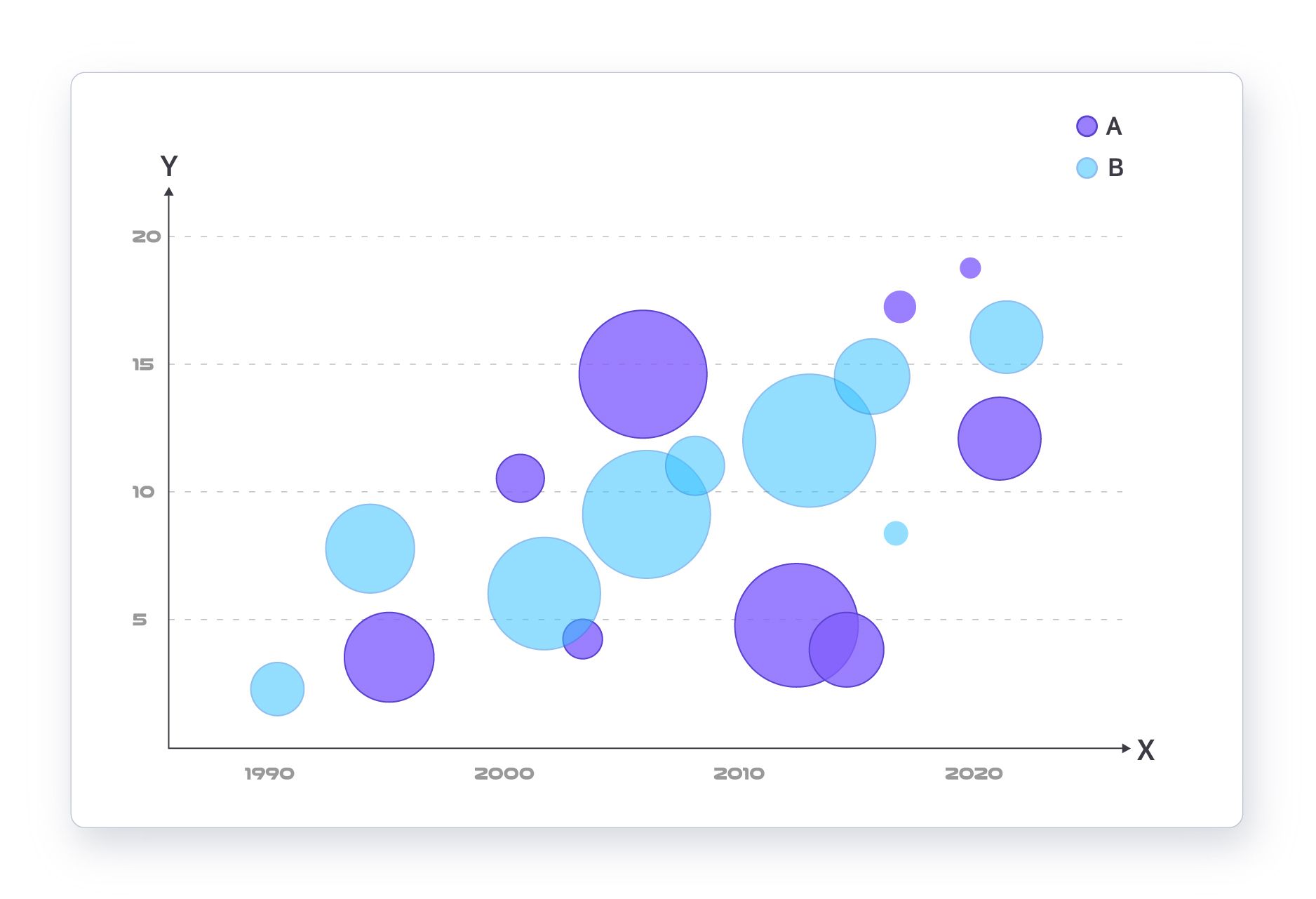
(7) 공간 시각화
공간 시각화는 데이터가 지리적 위치와 연관되어 있을 시 실제 지도 위에 데이터를 표현하는 것이다.
예를 들어 지역별 인구수 혹은 지역별 교통 인프라의 수준등을 시각화 하기에 적합하다.
공간 시각화 방식으로는 대표적으로 4가지 방식이 존재한다
- 도트맵 -도트맵 방식은 지리적 위치에 동일한 크기의 점을 찍어서 해당 지역의 데이터 분포나 패턴을 표현하는 기법이다.
- 버블맵 -지도 위에 버블 차트 형식으로 데이터의 크기를 원의 크기를 이용해 표현하는 기법이다.
- 코로플레스맵 -데이터 값의 크기에 따라 색상의 음영을 달리하여 해당 지역에 대한 값을 시각화하는 기법이다.
- 커넥션맵 -지도에 찍힌 점들을 선으로 연결하여 지리적 관계를 표현한다.
(8) 박스 플롯
박스플롯이란 네모 상자 모양에 최댓값과 최솟값을 나타내는 선이 결합된 모양의 데이터 시각화 방식이다.
전체 값의 하위 25% ~ 75% 사이의 값은 네모난 상자로 나타낸다.
그리고 상자 위 긴 선은 상자 맨 위 값의 1.5배에 해당하는 값을 의미한다.
이를 이상치를 제외한 최댓값으로 본다.
아래로 뻗은 긴 선도 마찬가지로 상자 맨 아래 값의 1.5배에 해당하는 값을 의미하며 이상치를 제외한 최솟값으로 본다.
네모난 상자에 해당하는 영역을 IQR이라 하며 가로선은 50%지점을 의미한다.
박스플롯은 데이터 분포를 정형화시켜 정보를 축약한 것이다.
다음은 정규분포와 박스플롯의 관계이다.
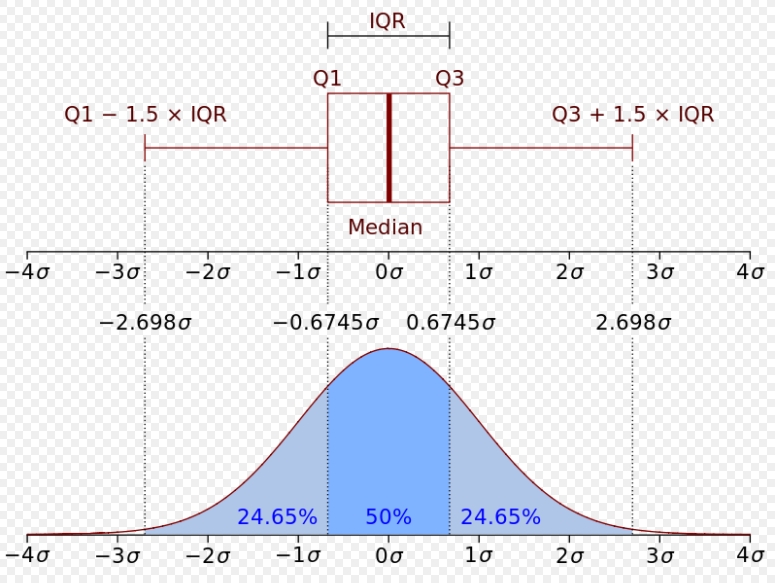
이상 데이터 탐색과 시각화에 관한 포스팅을 마치겠다.
